Exercice 17B
Enoncé :
A l'aide d'un logiciel de simulation, on peut étudier la composition du mélange d'un acide et de sa base conjuguée en fonction du pH.
On obtient ainsi le diagramme de distribution des espèces acide et basique du couple ion ammonium/ammoniac NH4+/NH3 pour une solution telle que : . . . c = [NH4+]f + [NH3]f = 5,00 . 10-3 mol.L-1.
a. Ecrire l'équation de la réaction de l'ion ammonium NH4+ avec l'eau.
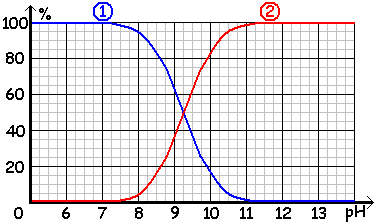
b. Identifier l'espèce chimique correspondant à chacune des 2 courbes.
c. Préciser pour quelle valeur du pH on a la relation : [NH4+]f = [NH3]f
d. En déduire le pKA, puis le KA du couple ion ammonium/ammoniac.
Solution :
a. L'équation de la réaction de l'ion ammonium NH4+ avec l'eau s'écrit :
NH4+(aq) + H2O(l)
NH3 (aq) + H3O+(aq)
b. La constante d'acidité KA du couple NH4+/NH3 associée à cette équilibre a pour expression :
KA = `([NH_3]_f * [H_3O^+]_f)/([NH_4^+]_f)`
. . . D'où :
log KA = log `([NH_3]_f * [H_3O^+]_f)/([NH_4^+]_f)` = log `([NH_3]_f)/([NH_4^+]_f)` + log [H3O+]
. . . D'où :
- log KA = - log `([NH_3]_f)/([NH_4^+]_f)` - log [H3O+]
. . . Sachant que par définitions : . . . pKA = - log KA et pH = - log [H3O+], . . . on obtient :
pKA = - log `([NH_3]_f)/([NH_4^+]_f)` + pH
. . . D'où :
log `([NH_3]_f)/([NH_4^+]_f)` = pH - pKA . . . (1)
. . . Conséquence : . . . log `([NH_3]_f)/([NH_4^+]_f)` > 0 . . . si . . . pH - pKA > 0
. . . . . . L'espèce basique NH3 est prédominante pour pH > pKA
. . . De même : . . . log `([NH_3]_f)/([NH_4^+]_f)` < 0 . . . si . . . pH - pKA < 0
. . . . . . L'espèce acide NH4+ est prédominante pour pH < pKA
. . . Conclusion :
. . . . . . L'espèce acide NH4+ est prédominante pour les valeurs faibles du pH. Elle est donc représentée par la courbe bleue.
. . . . . . L'espèce basique NH3 est prédominante pour les valeurs élevées du pH. Elle est donc représentée par la courbe rouge.
c. Lorsque les concentrations [NH4+]f et [NH3]f sont égales, on doit avoir 50 % de chacune des 2 espèces chimiques.
. . . D'après le diagramme de distribution, cela est réalisé lorsque les 2 courbes se coupent.
. . . On lit sur le diagramme de distribution, que les 2 courbes se coupent pour pH = 9,25.
d. Si : . . . [NH4+]f = [NH3]f . . . alors : . . . log `([NH_3]_f)/([NH_4^+]_f)` = log 1 = 0
. . . D'où, d'après la relation (1), : . . . pH - pKA = 0
. . . D'où :
pH = pKA
. . . Cette relation étant vérifiée lorsque pH = 9,25, on en déduit que : . . . pKA = 9,25
. . . Par définition, . . . KA = 10- pKA
. . . A.N. : . . . KA = 10- 9,25 = 5,6 . 10-10.