T.P.3 Analyse spectrale

 

A. Simulation sur Généris (p.52)

 

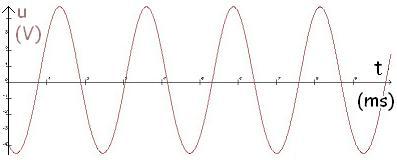
Sur Généris, on crée les tensions sinusoïdales u_n(t) d'amplitude `1/n` et de fréquence f_n = n . 440 Hz pour 1 ≤ n ≤ 10.

 

Puis, on crée les fonctions : . . u₁ + u₂ , . . u₁ + u₃ , . . u₁ + u₄ , . .u₁ + u₃ + u₅ + u₇ , . . u₁ + u₂ + u₃ + ... + u₁₀ .

 

On observe la forme des tensions obtenues et leur spectre.

 

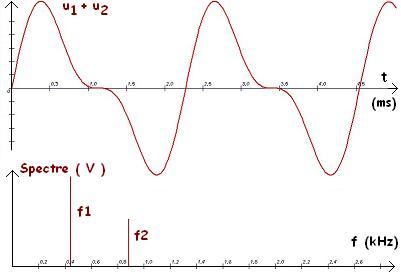
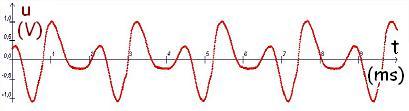
Représentation de la tension u1 + u2 et de son spectre

 

 

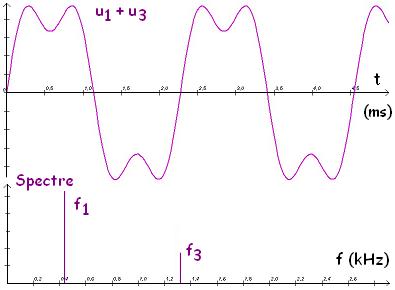
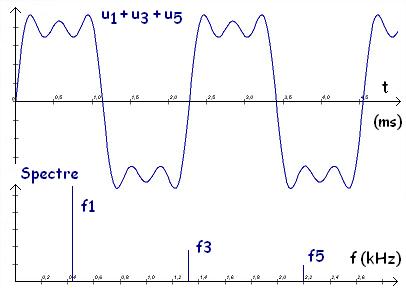
tension u1 + u3 et son spectre	tension u1 + u4 et son spectre

 

 

tension u1 + u3 + u5 et son spectre	tension u1 + u2 + ... + u10 et son spectre

 

 

B. Analyse spectrale de 3 sons (p.53)

 

A l'aide de Généris, on enregistre différents sons.

 

le diapason 440 Hz	un tuyau d'orgue	une corde métallique

 

Puis on réalise l'analyse spectrale de ces sons.

 

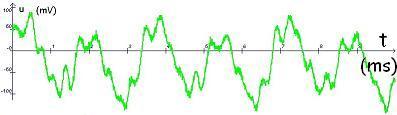
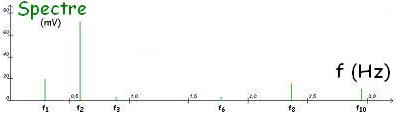
son du diapason
spectre de ce son

 

 

son du tuyau d'orgue
spectre de ce son

 

 

son d'une corde
spectre de ce son

 

 

C. Détermination d'une vitesse par Effet Doppler (p.55)

 

On enregistre le signal reçu par un récepteur d'ultrasons immobile ou en mouvement par rapport à l'émetteur.

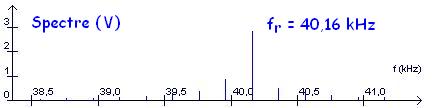
Puis, à l'aide de l'analyse spectrale, on détermine la fréquence du signal reçu.

 

. . . . . . . . Dispositif expérimental :

 

 

Emetteur et récepteur fixes
Ondes réfléchies par un écran en mouvement

 

La vitesse de l'écran est donnée par la relation : . . v = v_son . `(f_r - f_s)/(2 * f_s)`

. . . Remarque : . . Le facteur 2 apparaissant au dénominateur est dû à la réflexion des ondes sur un écran mobile.

 

. . . . . . . . A.N. : . . v = 340 . `(40,16 - 39,75)/(2 * 39,75)` = 1,76 m.s^-1.