T.P.17 La chute libre

 

Le TP commence par l'enregistrement vidéo de la trajectoire de billes en chute libre (soumises uniquement à leur poids pendant la chute).

On étudie les 3 cas suivants :

. . . . . . . - Bille lâchée sans vitesse initiale ;

. . . . . . . - Bille lancée avec une vitesse initiale horizontale ;

. . . . . . . - Bille lancée avec une vitesse initiale quelconque (composante verticale + composante horizontale).

 

Pour analyser ces mouvements, les trajectoires sont décomposées selon 2 axes (horizontal et vertical).

 

Enregistrement des trajectoires :

 

dispositif expérimental	webcam	ordinateur avec logiciel ExAO

 

 

Exploitation d'une vidéo :

 

Les enregistrements vidéo réalisés sont traités image par image, de façon à connaître la position de la bille au cours du temps pour les différentes trajectoires obtenues.

Traitement des enregistrements :

. . . . . . . - Ouvrir une vidéo avec le logiciel "Atelier scientifique" ;

. . . . . . . - Choisir une origine (ce choix est sans conséquence pour la suite) ;

. . . . . . . - Etalonner l'axe vertical ;

. . . . . . . - Choisir un repère orthonormé pour les mouvements non rectilignes ;

. . . . . . . - Commencer le Traitement (bouton vert) ;

. . . . . . . - Pointer la position de la bille sur chaque image ;

. . . . . . . - Arrêter le Traitement (bouton rouge).

 

 

Tableau des données :

 

Sous l’onglet Tableau (en bas à droite) on trouve les coordonnées des positions successives de la bille.

 

Image d'un tableau

 

 

Graphiques x(t) et y(t) :

 

Cliquer sur l’onglet Graphique (en bas à droite).

Cliquer sur les grandeurs ( x ou y) dont on veut afficher le graphique en fonction du temps.

 

. . . .

 

Vitesses instantanées v_x(t) et v_y(t) :

 

Ajouter, dans le Tableau, une colonne V_y (vitesse instantanée selon l'axe vertical) ;

Dans cette colonne entrer la formule : . . . . . V_y(n) = `(y(n+1) – y(n-1))/(t(n+1) – t(n-1))`

Si besoin, faire de même pour V_x (vitesse instantanée selon l'axe vhorizontal).

 

Accélérations instantanées a_x(t) et a_y(t) :

 

Ajouter, dans le Tableau, une colonne a_y (accélération instantanée selon l'axe vertical) ;

Dans cette colonne entrer la formule : . . . . . a_y(n) = `(V_y (n+1) – V_y (n-1))/(t(n+1) – t(n-1))`

Si besoin, faire de même pour a_x (accélération instantanée selon l'axe horizontal).

 

Lois horaires :

 

Cliquer sur l’onglet Graphique et faire afficher successivement les graphes x(t), y(t), v_x(t), v_y(t), a_x(t) et a_y(t).

 

. . . .

 

Vérifier que les graphes obtenus expérimentalement sont en accord avec les lois horaires établies en cours, c'est-à-dire vérifier que ces graphes ont bien la forme linaire ou parabolique prévue.

 

Modélisation du mouvement :

 

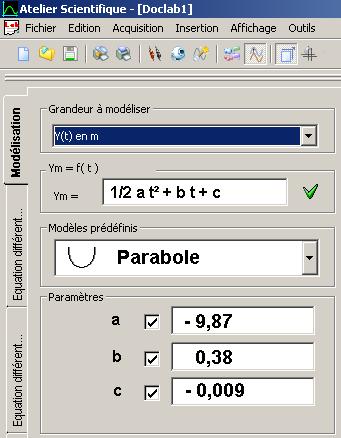
Il est également possible de modéliser une loi horaire c'est-à-dire de vérifier si le graphe est celui d'une droite affine ou d'une parabole (par exemple) :

Exemple pour le graphe y(t) :

 

 

Conclusion :

 

Selon l'axe vertical, le mouvement est accéléré (la vitesse de chute augmente).

Le logiciel utilisé indique que l'accélération est de 9,87 (m/s²) vers le bas.

Ceci est cohérent avec la présence d'une force verticale non compensée (le poids) pendant la chute.

L'accélération mesurée expérimentalement (9,87 m/s²) est égale, à moins de 1% près, à l'accélération théorique de la pesanteur (9,81 m/s²).

 

Selon l'axe horizontal, le mouvement est uniforme (la vitesse horizontale est constante).

Ceci est cohérent avec le Principe d'inertie, car aucune force horizontale n'agit pendant la chute.

 

Les mouvements étudiés sont donc en parfait accord avec l'étude théorique faite en cours.